Skip to content

Transformer understanding

The transformer model was introduced in 2017 by Google's paper Attention Is All You Need.

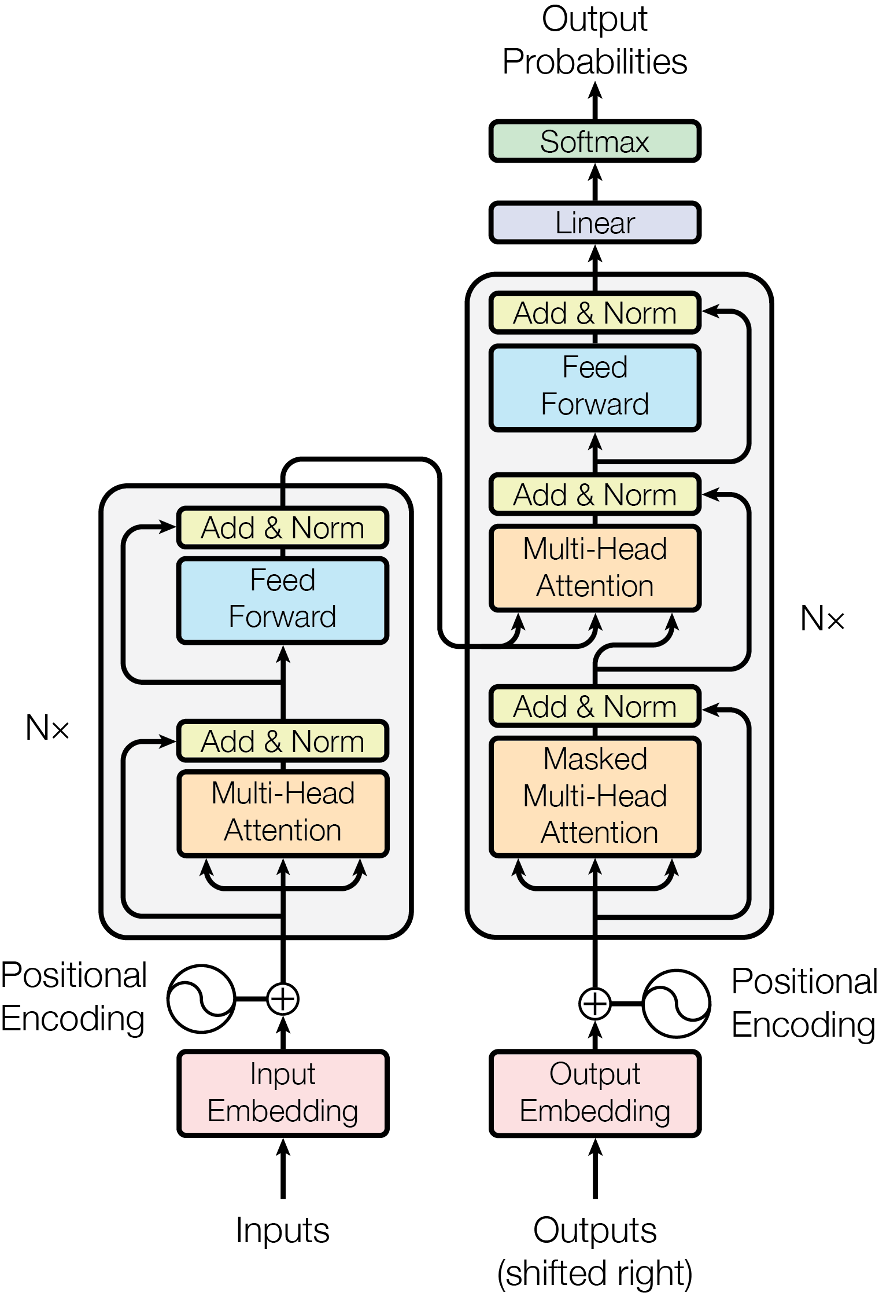
Below image shows the architecture of the transformer model which is from the Google's paper Attention Is All You Need.

The model has 6 layers.

Encoder and Decoder Stacks

  • The output of l layer is the input of l+1 layer.

  • The left side is a stack of N = 6 identical encode layers.

    Each layer has two sub-layers. The first is a multi-head self-attention mechanism, and the second is a simple, positionwise fully connected feed-forward network.

  • The right side is a stack of N=6 identical decode layers.

    The decoder inserts a third sub-layer, which performs multi-head attention over the output of the encoder stack.

  • In each layer, there is a residual connection around each of the two sub-layers, followed by layer normalization, to make sure the information such as position encoding will be not lost. The output of each sub-layer is LayerNorm(x + Sublayer(x)), where Sublayer(x) is the function implemented by the sub-layer itself.

  • To facilitate these residual connections, all sub-layers in the model, as well as the embedding layers, produce outputs of dimension \(d_{model}=512\).

Encoder

Input Embedding

Convert the input token into dimension \(d_{model}=512\).

Positional Encoding

To encoding the positional into the token's model. The following formula is used to calculate the positional.

\[ PE_{(pos 2i)} = sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) \]
\[ PE_{(pos 2i+1)} = cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) \]

Multi-Head Attention

For each input vector \(d_{model}=512\) of token \(X_n\):

\[ pe(x_n)=[d_1=9.09297407e^{'}01, d2=-4.16146845e'01,...,d_{512}=1.00000000e+00] \]

Each head's output: \(Z=(Z_0, Z_1, Z_2, Z_3, Z_4, Z_5, Z_6, Z_7)\)

Final output: \(MultiHead(output)=Concat(Z_0, Z_1, Z_2, Z_3, Z_4, Z_5, Z_6, Z_7)=x, d_{model}\)

In each head attention, word matrix has 3 represents.

  • Query matrix \(Q\), dimension \(d_q=64\)
  • Key matrix \(K\), dimension \(d_k=64\)
  • Value matrix \(V\), dimension \(d_v=64\)

In the original transformer model, the attention can be described as,

\[ Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{D_k}})V \]

Add & Norm

Normalization can be described as \(LayerNormalization(x+Sublayer(x))\)

  • \(Sublayer\) is the the sub-layer itself, \(x\) is the input.
  • vector \(v\) = \(x\) + \(Sublayer\)

There are many ways to do layer normalization, one way is:

\[ LayerNormalization(v)=\gamma\frac{\nu-\mu}{\sigma} + \beta \]
  • \(\mu=\frac{1}{d}\sum_{d}^{k=1}\nu_k\)
  • \(\sigma^2=\frac{1}{d}\sum_{d}^{k=1}(\nu_{k-\mu})\)

Feed Forward

The dimension is \(d_{model}=512\),

\[ FFN(x)=max(0, xW_1 + b_1)W_2 + b_2 \]

Decoder

There is also a residual connection around each of the two sub-layers, followed by layer normalization:

\[ LayerNormalization(x+Sublayer(x)) \]

Input Embedding & Positional Encoding

They are the same as encoder.

Masked Multi-Head Attention

The sub-layer input is \(Input\_Attention=(Output\_decoder\_sub\_layer - 1(Q), Output\_encoder\_layer(K,V))\).

FFN Sub-Layer, Add & Norm and Linear

The transformer will only generate an output sequence of an element:

\[ Output\_sequence=(y_1, y_2, ..., y_n) \]

The liner will generate an output sequence, it will vary based on model, but it will approach \(y=w*x+b\).

\(w\) and \(b\) are learnable parameters.

to be continued...